希尔排序——重温排序（二）

上篇文章提到，插入排序在待排序列基本有序的时候，效率会好很多。这篇文章介绍的希尔排序，其基本思想就是先让序列基本有序，然后再进行插入排序。

一、算法描述

希尔排序先将待排序列进行分组，分别进行插入排序，间隔为 gap 的元素为一组。待各组排序完成后，逐渐缩小 gap 的值，重复分组排序过程，直到 gap 值缩小为1，即对整个序列进行一次插入排序。

gap 一般先取 n / 2 ，然后逐步 gap = gap / 2 ，直到 gap 等于1。

二、图示举例

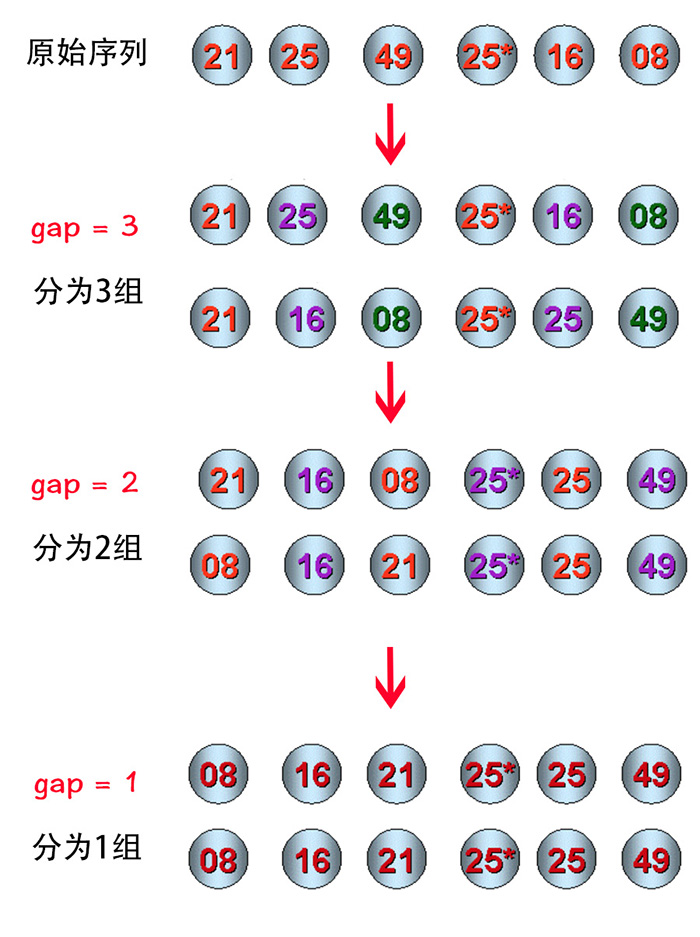
下面来看一个希尔排序的图示，注意观察两个的关键字为25的元素，思考一下希尔排序的稳定性。

三、算法实现

C语言版本代码奉上。

void shellSort(int list[], int count) {
    for (int gap = count / 2; gap >= 1; gap /= 2) {
        for (int i = 0; i < gap; ++i) {
            insertSort(list, count, i, gap);
        }
    }
}

void insertSort(int list[], int count, int head, int gap) {
    int temp, i, j;
    for (i = head + gap; i < count; i += gap) {
        temp = list[i];
        for (j = i - gap; j >= head; j -= gap) {
            if (list[j] <= temp) {
                break;
            }
            list[j+gap] = list[j];
        }
        list[j+gap] = temp;
    }
}

可以看到，希尔排序不过是一个不断进行插入排序的过程。在这个过程中，去不断地调整序列的头位置 head 和间隔 gap 的值。而这里用到的插入排序算法，跟之前相比做了一点小调整，修改了待排元素的索引，加上了对应的 gap 偏移。

四、算法分析

• 开始的时候 gap 值较大，子序列中的元素较少，排序速度较快，而且元素一次移动的距离较大。
• 随着排序的进行， gap 值逐渐缩小，子序列中元素个数逐渐变多，但由于前面的排序结果，子序列基本有序，因此排序也很快。
• 从图示的例子中看出，两个关键字为25的元素，在排序前后，它们的相对位置已经发生变化，所以希尔排序是一种不稳定的排序。
• 希尔排序需要比较次数和移动次数约为 n ^ 1.3 ，当 n 趋于无穷时可减少到 n(log2(n))^2 。

五、总结

• 希尔排序的时间复杂度为 O( n(log2(n))^2 ) 。
• 希尔排序是一种不稳定的排序。